Optimizing Train Track Curves for Efficiency

Train travel efficiency is often limited by the geometric design of curved tracks, where speed constraints increase travel time. This project focuses on optimizing curve designs to minimize travel time while ensuring safety and accounting for real-world constraints.

The objectives included deriving a time equation for trains on curved paths, using optimization techniques such as the Euler-Lagrange equation and polynomial approximation, and developing computational tools to calculate travel time for various curve shapes.

Methods and Derivations

The methods involved formulating a time integral that incorporates curvature and speed constraints, solving it numerically with MATLAB for the Euler-Lagrange approach, and using Python’s SLSQP algorithm for polynomial approximation.

This is how we derived the equation that we used to determine the time along the curve, and some optimization techniques we used for differente types of functions.

Results

The results revealed that curve geometry has a significant impact on travel time, with even and odd powers of x displaying distinct behaviors due to differing displacement intervals. Optimized curves effectively minimized travel time while meeting all constraints, demonstrating the efficiency of the proposed methods. This work provides a foundation for further improvements in train travel and broader transportation systems.

Results for Polynomials

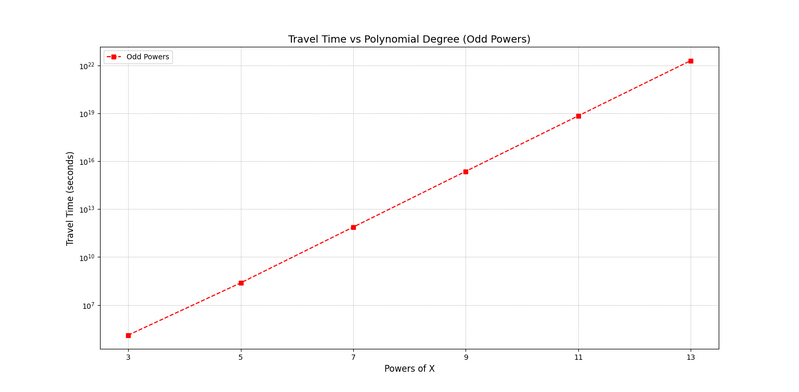
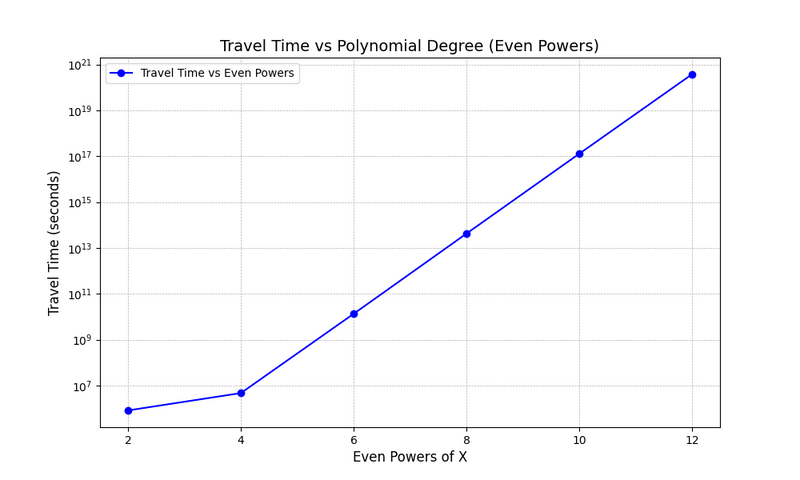
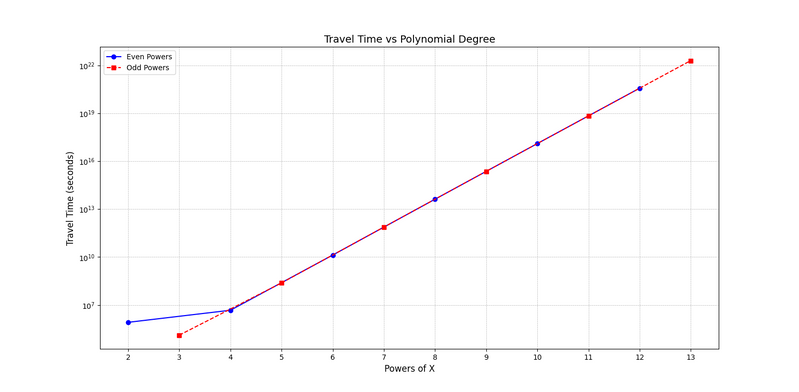
Results for Trigonometric Functions

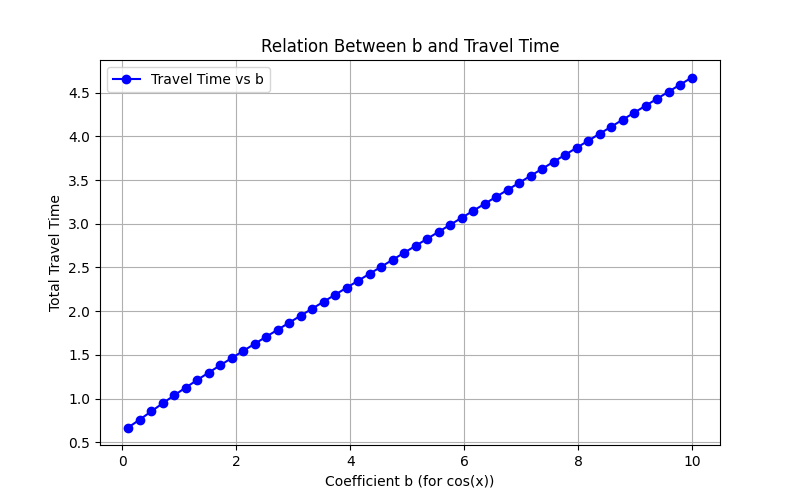
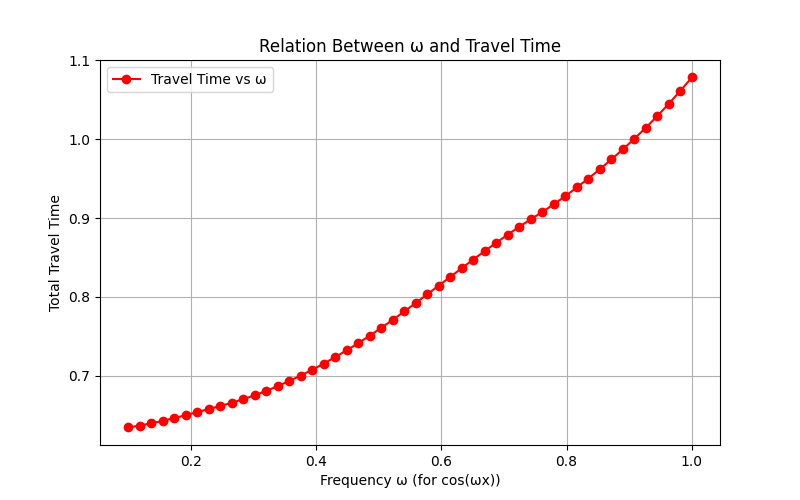
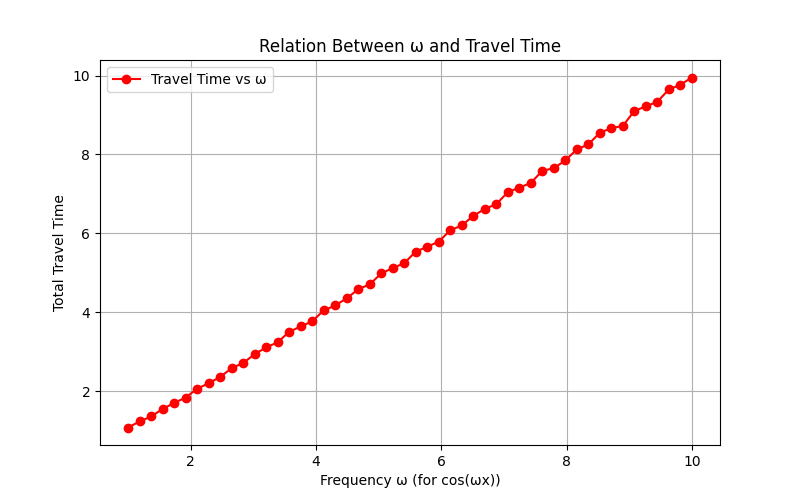
Circular Graphs

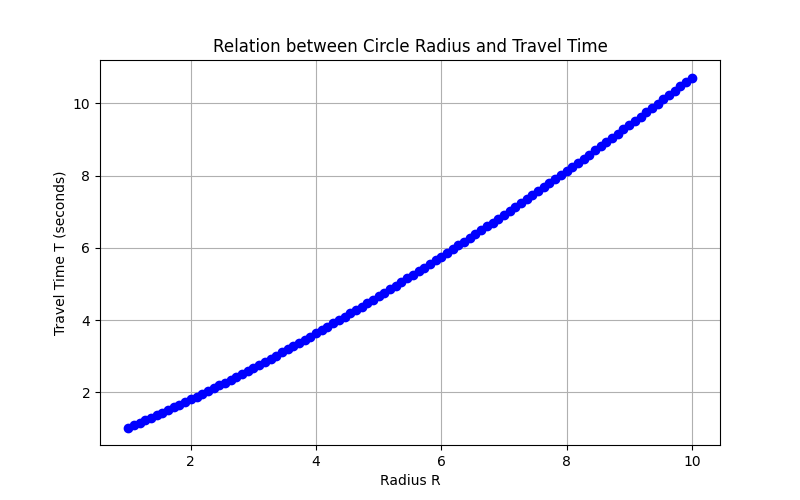
Cycloidal Graphs

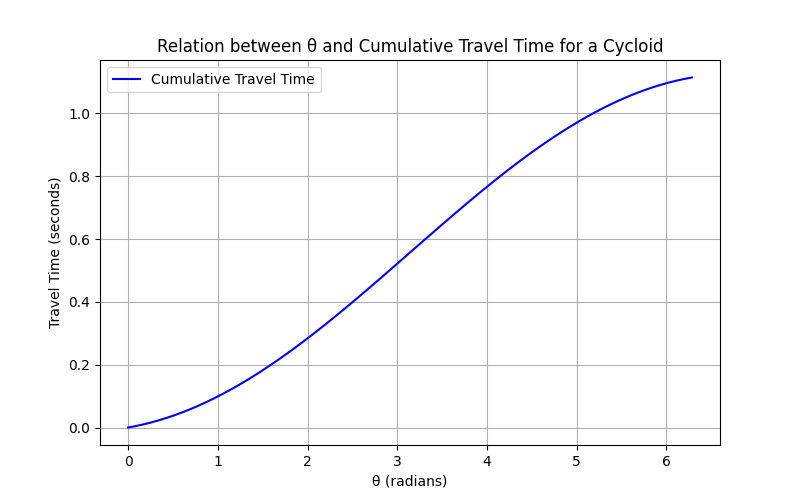
Conclusion

This research aims to meet our sustainability goals, as it meets some of the Sustainable Development Goals (SDGs). Meeting the 9th, 11th, and 12th goals by building more sustainable roads that saves energy, improving public transportation and urban planning, conserving the amount of used fuel, and making huge advancements in math optimization problems.